The Logic of Null Hypothesis Significance Testing

How does Hypothesis Testing work?

How does it work? Well, think for a moment about a jury trial. The defendant is firstly presumed innocent. Facts and evidence are presented before the court. The jury then decides if it is unlikely, beyond a reasonable doubt, that the defendant is innocent. If they decide that it is unlikely that the defendant is innocent, then they declare that the defendant is guilty. If they decide that there is not enough evidence to convince them that the defendant is guilty, then they declare that they find the defendant not guilty. We do not know if the defendant is truly guilty or innocent and so there are four possible outcomes, as can be seen in the following diagram.

Clearly, we would like to see as few innocent people as possible going to jail and we would also like to prevent criminals going free as much as possible. This requires us to have some kind of trade-off between being too lenient and being too strict with the level of evidence required to reject the assumption of innocence.

Hypothesis testing works in a similar manner. We start by assuming that the Null Hypothesis is true. The sample data provides the evidence. We then determine if it is unlikely, beyond some preset level, that the Null Hypothesis is true. If we decide that it is unlikely that the Null Hypothesis is true, we declare that we "reject the Null Hypothesis". If we decide that there is not enough evidence, then we declare that we "fail to reject the Null Hypothesis". Again, we do not know the truth about the Null Hypothesis; we can only make an inference based on the sample data.

In hypothesis testing, we ASSUME that the Null Hypothesis (or the hypothesis of no change) is true.

More formally, we examine the evidence and determine the probability of obtaining our result or one more extreme under the assumption that the Null Hypothesis is true, i.e. $Pr\left(\text{Data}|H_{0}\text{ true}\right)$ . If the probability is so small that the result is unlikely to have occurred simply by chance, we reject the assumption that the Null Hypothesis and conclude that the evidence suggests that the Alternate Hypothesis is supported. Note that we do not say that we have proved anything.

Null Hypothesis Significance Testing, regardless of the test statistic used (e.g. $Z$ , $\chi^{2}$ , $t$ , $F$ , etc.), can be broken down into four steps:

State the hypotheses, significance level ( $\alpha$ ), any assumptions/definitions
Based upon the sample data, compute an appropriate decision statistic
Reject or Fail to Reject the Null Hypothesis. State your conclusion.
Where appropriate, conduct a suitable Post-Hoc test and interpret it

Depending on your discipline or the journal you intend to publish with, you may also be required to compute and state other items like an estimate of the Effect Size. Your lecturers, tutors, supervisors or journal editors will be able to provide you with a better guide as to what else you may be required to do whenever you conduct a Hypothesis test; however, the steps above are reasonably close to universal, despite what some textbooks may say.

Just like in the jury trial, there are four possible outcomes depending on the true situation and the decision we make in the test. The following illustrates these possible outcomes.

Let’s take a closer look at each of these steps.

State the hypotheses, significance level (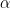 $\alpha$ ), any assumptions/definitions

Hypotheses

The hypotheses are the Null and Alternate hypotheses. A Hypothesis is a definitive statement about a population parameter in present or past tense taken from the research question. Typically, there are two hypotheses (see note 1), one of which is called the Null Hypothesis (denoted by $H_{0}$ ). The Null Hypothesis (or the hypothesis of no change, no association, no difference or no effect, hence "null") states the status quo and is testable. For example, if the research question is about the effect on emission levels of a new fuel additive, then the Null Hypothesis would state that the emission levels remain unchanged with the new fuel additive. The other hypotheses are logical opposites to the Null Hypothesis, and if there is only one other hypothesis, it is called the Alternate Hypothesis (denoted by $H_{A}$ – see note 2). The Alternate Hypothesis is a logical negation of the Null Hypothesis, e.g. the Null Hypothesis says the population mean is equal to ten, the Alternate Hypothesis says that the population mean is not equal to ten (see note 3).

The Alternate Hypothesis can also indicate the direction of interest, for example, if we are testing the fuel additive and the effect on emissions, we most likely don’t want to use the additive if it makes emissions worse. In such a case, the Alternative Hypothesis may state that population parameter is less than (or greater than) the specified value. Such alternative hypotheses are often referred to as a directional hypothesis. Typically, however, it is preferable to use a non-directional Alternate Hypothesis and determine the direction of any change after completing the hypothesis test. The following table shows the three possible sets of hypotheses for the population mean ( $\mu$ ).

	Non-directional	Directional
	(two-tailed)	(one-tailed, lower)	(one-tailed, upper)
Null Hypothesis	$H_{0}$ : $\mu = \mu_{0}$	$H_{0}$ : $\mu = \mu_{0}$	$H_{0}$ : $\mu = \mu_{0}$
Alternate Hypothesis	$H_{A}$ : $\mu \neq \mu_{0}$	$H_{A}$ : $\mu < \mu_{0}$	$H_{A}$ : $\mu > \mu_{0}$

Note: the symbol $\mu_{0}$ represents the value of the population mean under the Null Hypothesis. So if the Null Hypothesis states that the population mean equals 10, then $\mu_{0}=10$ and therefore (in symbols) the Null Hypothesis would be $H_{0}$ : $\mu = 10$ .

Significance level

The significance level (denoted by $\alpha$ ), which is sometimes called alpha level or Type I Error level, is our level of reasonable doubt and it is set a priori of any collection of sample data. It is the level of "unusualness" we require of the evidence before we conclude that the Null Hypothesis is not supported. This value is also the probability that we will make a Type I Error, that is, rejecting the Null Hypothesis when it is, in fact, true (i.e. like sending an innocent person to jail). Another way to think about it is, "What proportion of people will die if I am wrong". As such we want this value to be as small as possible, however, the smaller we make it, the bigger we make the probability of making a Type II Error (denoted by $\beta$ ). A Type II Error is when we fail to reject a Null Hypothesis that is false (i.e. like letting a criminal go free), which can be thought of as "The proportion of people whose death could have been prevented if I am wrong". Again we want this value to be as small as possible, and so we have to make some sort of trade-off.

Similar to how $\alpha$ describes how unusual a result we require to conclude that the Null Hypothesis is not supported, so $1 - \beta$ describes the Power of our test to make the correct decision when the Null Hypothesis is in fact false. It is important to recognise though that we do not "set" $\beta$ in the same way we specify $\alpha$ . The value of $\beta$ is determined more by how close our Null Hypothesis is to the true real-world situation and by the sample size we take. The bigger the sample size and the further apart our Null Hypothesis is from the truth, the smaller $\beta$ will be. We would not deliberately pick a Null Hypothesis that was vastly different from the status quo, that would be contrary to what the Null Hypothesis represents. Simply taking more samples can introduce other problems, such as higher costs, and so we again make some sort of trade-off in an effort to maximise the power of our test.

In general, non-life threatening research we typically set our significance level to 5% (i.e. $\alpha = 0.05$ ) or even 1% in some cases(i.e. $\alpha = 0.01$ ). In research that has potentially fatal consequences, e.g. drug trials, the alpha level is usually much smaller (e.g. 1 in 1 million, i.e. $\alpha = 0.000001$ ). The level you use can also depend on the accepted typical values for research in your discipline. The fallback position when you are unsure is to use an alpha level of 5% because that is what the great statistician of the early 20th century Sir R. A. Fisher said to use. An alpha level of 5%, under the Normal distribution, is roughly equivalent to requiring your sample to produce a sample mean more than 2 standard errors away from the Null Hypothesised mean value. These days we have powerful computers and can work with many different types of distributions, but the 5% fallback remains in place simply because "that is what we have always done".

Assumptions and definitions

All hypothesis tests have at least two assumptions behind them and depending on which test statistic you need to compute (e.g. $Z$ , $\chi^{2}$ , $t$ , $F$ , etc.) there may be other assumptions which need to be met in order for the results to be valid. The first is that the sample data is Representative of the population of interest. There is little point conducting a hypothesis test on data concerning Zebras if you want to make an inference about the effect of a new fuel additive on car emissions. Equally, there is also little point in conducting a hypothesis test on emissions data taken from race cars if you want to make an inference about regular cars. As such, you need to look at the Research Design to see how the study has collected the sample data. If there is a clear bias in the sampling technique or if the samples are not drawn from the population of interest, then this assumption has been violated and you should not proceed with the test.

The second assumption of almost every hypothesis test is what is called the Independence assumption and states that it is assumed that each of the samples are independent of one another. To check that this assumption has not been violated, again you should look closely at the Research Design to see how the samples were obtained. Independence means, in statistical terms, that for any two events, knowing that one event has occurred does not influence the probability of the other event occurring, i.e. the conditional probability of each event is equal to its unconditional probability ( $Pr(A|B)=Pr(A)$ AND $Pr(B|A)=Pr(B)$ ).

The last part of this step is to define any terms used or special symbols. For example, if you are conducting a hypothesis test using patient BDI scores, you need to define what a BDI score is. Alternatively, you might be conducting a hypothesis test comparing males and females, and so it is important to identify for your reader which symbol(s) represent the variables for males and which represent the variables for females. There is no need to state a definition for $\alpha$ , $H_{0}$ or any other standard items of hypothesis testing, you only need to define those which would be unclear to a reader not intimately involved in your research.

Based upon the sample data, compute an appropriate decision statistic

There are three types of decision statistic methods that can be used, namely:

The Critical Value method
The p-value method
The Confidence Interval method

The choice of decision statistic method greatly depends on the kind of statistical test you are performing and the reporting requirements of your discipline. In most cases, however, the Confidence Interval method is preferred over the p-value method. The Critical value method should only be used as a last resort as it provides the least amount of information to your reader.

The Critical Value method

The Critical Value method is the simplest method for a making a decision. Under this method, we find the critical value(s) under the Null Hypothesis distribution that represents the cut-off point(s) for the rejection region. If we are conducting a non-directional hypothesis test (i.e. two-tailed test), then we need two critical values, each cutting off $\alpha \div 2$ of the Null Hypothesis distribution. If we are conducting a directional hypothesis test (i.e. one-tailed test), then we need the critical value that cuts off $\alpha$ of the Null Hypothesis distribution in the appropriate tail. The following table shows these values for the Standard Normal distribution with $\alpha = 0.05$ . When using this method, the critical value(s) is(are) the yardstick we use in making our decision to either "Reject" or "Fail to Reject". We compare our obtained test-statistic (see “The p-value method” for more detail on test-statistics) to this yardstick.

	Non-directional	Directional
	(two-tailed)	(one-tailed, lower)	(one-tailed, upper)
Null Hypothesis	$H_{0}$ : $\mu = \mu_{0}$	$H_{0}$ : $\mu = \mu_{0}$	$H_{0}$ : $\mu = \mu_{0}$
Alternate Hypothesis	$H_{A}$ : $\mu \neq \mu_{0}$	$H_{A}$ : $\mu < \mu_{0}$	$H_{A}$ : $\mu > \mu_{0}$
Critical Value(s)	$\pm 1.96$	$- 1.645$	$+ 1.645$
Graphically

The p-value method

This decision method is more informative to your reader than the critical value method and tends to dominate the research literature in most disciplines at present. Under this method, the Significance Level ( $\alpha$ ) acts as our yardstick. The process for this method is as follows, we first calculate a test statistic, based upon our sample data and then compute the probability of obtaining this test statistic or one more extreme under the Null Hypothesis distribution, i.e.:

$Pr\left(\text{Test Statistic or more extreme } | H_{0} \text{ true}\right) = ?$

This probability is what we call our p-value. This is a conditional probability, not the probability that the Null Hypothesis is true. In fact, as is seen in the conditional probability above, in hypothesis testing we assume that the Null Hypothesis is true, so $Pr\left(H_{0} \text{ true}\right)=1$ .

This might get you thinking that hypothesis testing is a waste of time since we really want to know what is the probability that the Null Hypothesis is true. Hypothesis testing is certainly not a waste of time; rather we have to recognise the limitations of what hypothesis testing can do and be careful in our interpretations (see Ovens (2018) for some common misconceptions).

By way of comparison, we know that jury trials are not perfect and we recognise that sometimes an innocent person goes to jail or a criminal walks free. Jury trials also presume that the defendant is innocent at the start of the trial, the evidence is presented, and the jury tries to figure out $Pr\left(\text{Evidence presented }|\text{ Defendant is innocent}\right)$ , but that doesn’t mean jury trials are a waste of time because they start by assuming $Pr\left(\text{Defendant is innocent}\right)=1$ and they can’t actually determine $Pr\left(\text{Defendant is innocent}\right)$ .

So the p-value is a conditional probability, namely the probability of obtaining this test statistic or one more extreme under the Null Hypothesis distribution, but what is the test statistic? Well, that depends on the form of hypothesis test you are doing, in general; however, most test-statistics have the following form:

$\text{Test Statistic } = \dfrac{\text{Sample Statistic }-\text{Null Hypothesised Value of Population Parameter}}{\text{Standard Error of the Sampling Distribution}}$

To help illustrate the p-value method, the figure below shows a two-tailed hypothesis test where the Null Hypothesis distribution is a Standard Normal distribution with $\alpha = 0.05$ . The critical values are $\pm 1.96$ (marked and shaded in dark-blue) and the p-value of $0.0186$ is shown shaded in light-blue (along with the corresponding Null Hypothesis distribution values marked).

The Confidence Interval method

Like the test statistic in the p-value method, this method depends on the hypothesis test you are performing, and in some cases, you would be very unlikely to compute the Confidence Interval. The general form, however, of a Confidence Interval is:

$\text{Sample Statistic }\pm\text{ Margin of Error}$

Where the Margin of Error is given by:

$\text{Margin of Error }=\text{ Critical Value of Null Hypothesis distribution }\times\text{ Standard Error term}$

Note: the "Standard Error term" is the term representing the "Standard Error of the Sampling Distribution" that is used in calculating the test statistic.

Confidence Intervals are somewhat misnamed. Unfortunately, the word "Confidence" implies some level of certainty or belief in our obtained interval. It is not unusual to see researchers write in their papers, "We are 95% confident that the true population mean is between 123.6 and 127.8", when what they should write is, "We obtain a 95% Confidence Interval for the true population mean of (123.6, 127.8). Ninety-five per cent of intervals obtained in this manner would capture the true population mean." It may not seem obvious to you, but there is a profound difference between these two statements (see this page for more details).

When using the Confidence Interval method, the value of the population parameter of interest under the Null Hypothesis acts as our yardstick. Under this method, we look to see if our obtained confidence interval for the population parameter of interest captures the Null Hypothesised value in order to make our decision to either "Reject" or "Fail to Reject" the assumption that the Null Hypothesis is true.

Reject or Fail to Reject the Null Hypothesis. State your conclusion.

Before we make a decision to "Reject" or "Fail to Reject" the assumption that the Null Hypothesis is true, we must understand how the decision statistic was determined. The appropriate decision statistic was determined given the Null Hypothesis is true, so much like in a jury trial, we have to decide if that is enough evidence to reject the assumption that the Null Hypothesis is true. In other words, if the decision statistic is unusual enough for us to conclude that it is unlikely to occur by chance, we conclude that it is unlikely the Null Hypothesis is true and so, therefore, the Null Hypothesis is not supported by the evidence presented by our sample data. For the decision statistic to be "unusual enough" for us to conclude that the Null Hypothesis should be rejected, we use our decision method’s yardstick that we defined at the very beginning of our test: (1) the Critical Value; (2) our Significance Level ( $\alpha$ ); or, (3) the Null Hypothesised value. Then we can make our decision, (1) by comparing our obtained Test Statistic to the Critical Value; (2) by comparing our obtained p-value to $\alpha$ ; or, (3) by noting if our Confidence Interval captures our Null Hypothesis value.

Comparing our obtained Test Statistic to the Critical Value

In this type of decision, we compare our Test Statistic to the Critical Value (in general obtained from a table of the distribution model). If our obtained Test Statistic is more extreme than the Critical Value then we Reject the Null Hypothesis, otherwise, we Fail to Reject the Null Hypothesis. This is the simplest form of decision making for a Hypothesis test.

Comparing our obtained p-value to 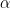$\alpha$

Putting it very simply, in this type of decision:

If $p < \alpha$ we Reject the Null Hypothesis, otherwise, we Fail to Reject the Null Hypothesis (see note 4).

This is the most common form of decision making for a Hypothesis test in the research literature of most disciplines. Most statistical packages, such as R or SPSS will produce a p-value as part of the output for a Hypothesis test.

Noting if our Confidence Interval captures our Null Hypothesis value

This type of decision is becoming more common as researchers begin to appreciate the information a Confidence Interval provides. In this type of decision, we look to see if our obtained Confidence Interval "captures" the Null Hypothesised value of the population parameter. If the Confidence Interval does not capture this value then we Reject the Null Hypothesis, otherwise, we Fail to Reject the Null Hypothesis.

A good way to envisage these forms of decision making is to think about the fence around a property. The fence represents the Critical Value of the test, whilst in this analogy, you will represent the Test Statistic. Suppose you are arrested on suspicion of trespassing (i.e. a sample is taken).

The judge will ask you which side of the fence did the police catch you on. If you are on the wrong side of the fence you will be found guilty (i.e. Reject the Null Hypothesis) otherwise you will be found not guilty (i.e. Fail to Reject the Null Hypothesis) (decision method 1).

The judge might also ask how far from the centre of the roadway were you when you were caught to determine the level of evidence that you were not trespassing (i.e. p-value). If the level of evidence that you were not trespassing is very small, the judge will find you guilty (i.e. Reject the Null Hypothesis) otherwise you will be found not guilty (Fail to Reject the Null Hypothesis) (decision method 2).

The judge might also estimate how fast you could run and guess that when you heard the sirens you started running, meaning that you could have been either much further away from the centre of the roadway or much closer to it when you heard the sirens. If the judge believes that it was not possible for you to be anywhere near the centre of the road, you will be found guilty (Reject the Null Hypothesis). If, however, the judge believes that it was possible you could have simply run across the centre of the roadway, then you will be found not guilty (Fail to Reject the Null Hypothesis) (decision method 3).

Note: There are various terms used for the decision to "Fail to Reject the Null Hypothesis". When textbooks or research literature talk about "Retaining" or "Accepting" the Null Hypothesis, it does not mean that the Null Hypothesis is true, it just means there is not enough evidence in the sample data to Reject the Null Hypothesis. This is just like when a jury concludes that there is not enough evidence to find a defendant "Guilty", so they say that the defendant is "Not Guilty". The jury is not saying that the person is innocent, just that there is not enough evidence to reject the presumption of innocence.

Having made our decision about the Null Hypothesis, we need to state that decision in a way that other readers of our research can understand. In general this will be something like:

If we Reject the Null Hypothesis:
We Reject H₀ with Test Statistic = …, p = … and α = ….

If we Fail to Reject the Null Hypothesis:
We Fail to Reject H₀ with Test Statistic = …, p = … and α = ….

Once we made our decision about the Null Hypothesis, we need to state what that decision implies about the Alternate Hypothesis. Typically this is something like:

If we Reject the Null Hypothesis:
The sample data provides statistically significant evidence that . . .

If we Fail to Reject the Null Hypothesis:
The sample data does not provide statistically significant evidence that . . .

We use the term statistically significant to distinguish the fact that our result, whilst significant in terms of the statistics, may not be practically significant. For example, we may invent a new drug treatment for headaches that is statistically significantly faster acting than the present best treatment, but it costs more than the present treatment and is only 20 seconds faster than the present treatment. Obviously, it is not much of a practical improvement, and it is unlikely that many people would want to pay more to relieve their headache 20 seconds faster than the present best treatment.

Where appropriate, conduct a suitable Post-Hoc test and interpret it

After you have determined whether or not you should Reject the Null Hypothesis, you may be able to provide your reader with more information by conducting a suitable post-hoc (i.e. "after the fact") test. For example, if you have used the p-value method for your test, it is usually a good idea to also compute a Confidence Interval and report it. Equally, in some forms of hypothesis tests, if you Reject the Null Hypothesis then all you know is that "at least one is different", but not which one(s). A post-hoc test in those cases allows you to identify the one(s) that are different.

Notes

1. In some advanced forms of hypothesis testing it is possible to have more than two hypotheses; however, the research literature usually involves only two for any single test — the paper may have multiple tests though.

2. Some texts will use the notation of $H_{1}$ for the Alternate Hypothesis. This author prefers to use the notation of $H_{A}$ to stand for all possible alternate values and $H_{1}$ , $H_{2}$ , etc. to stand for a particular alternate value (such as when conducting Bayesian inference).

3. In some cases, you may only wish to test if the parameter has changed in a particular direction. Generally, in this author’s opinion, it is better to test if the value is statistically significantly different from the value under the Null Hypothesis and determine the direction of change post-hoc. This helps to reduce the chance of making a Type I error and also allows you to detect if there has been a statistically significant change in the opposite direction than anticipated which may be a helpful indicator of either experimental error (e.g. scales not calibrated), theoretical error (e.g. assuming the wrong direction) or computational error (e.g. values have the wrong signs or other data entry errors).

4. Your lecturer might state this as "If $p \leq \alpha$ we Reject the Null Hypothesis, otherwise, we Fail to Reject the Null Hypothesis", it just depends whether they like to be conservative or take a bit more risk, but since the probability that your test statistic would result in a p-value equal to your significance level ( $\alpha$ ) is practically zero, it is a bit of a moot point.

CITE THIS AS:
Ovens, Matthew. “The Logic of Null Hypothesis Significance Testing”. Retrieved from YourStatsGuru.

First published 2018 | Last updated: 2 November 2024